Pedagogia Sperimentale On line - Prof. Roberto Trinchero

Correlazione tra variabili

Quando le variabili coinvolte nell’ipotesi sono entrambe cardinali, ad esempio “al crescere del numero delle ore di studio cresce il voto in matematica”, è possibile utilizzare il concetto di correlazione tra variabili. Supponiamo di avere 6 soggetti sottoposti a 2 prove oggettive, nelle quali hanno ottenuto i seguenti punteggi grezzi:

E possibile rappresentare i soggetti su un piano cartesiano dove la coordinata X è data dal punteggio ottenuto dal soggetto nel test X e la coordinata Y è data dal punteggio ottenuto dal soggetto, ad esempio, nel test Yd. Questo diagramma è detto diagramma a dispersione o scatterplot.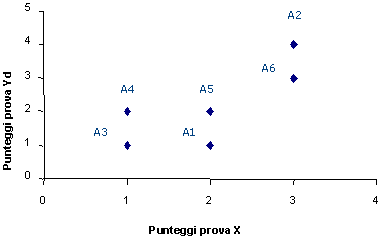

E’ possibile a questo punto definire un modello teorico, ossia una funzione matematica, che approssimi la nube di punti. Ad esempio: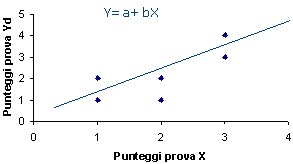

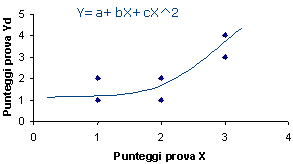
Se il modello teorico è lineare l’operazione di individuare una retta che approssimi al meglio la nube di punti è detta regressione lineare. Se il modello teorico utilizza una funzione non lineare si parla di regressione non lineare, che può essere ad esempio parabolica, logistica, ecc.

Il modello teorico ha una sua bontà di adattamento, che indica quanto è buona l’approssimazione del modello stesso alla nube di punti. La bontà di adattamento, qualunque sia il modello, è data dalla somma dei quadrati dei residui, ossia delle distanze tra i punti della nube e la loro previsione data dal modello teorico, misurate in verticale per ciascuno dei punti della nube. La retta che minimizza la somma dei quadrati dei residui è quella che garantisce la miglior bontà di adattamento possibili e si chiama retta di regressione.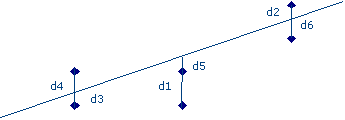

La retta che minimizza la somma dei quadrati dei residui ha coefficiente di regressione b pari a: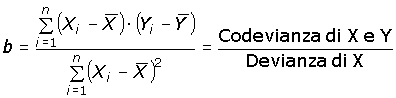

b è uguale al rapporto tra la devianza congiunta di X e Y (data dal prodotto degli scarti delle coordinate dei rispettivi punti dalle medie di X e di Y), detta codevianza di X e Y, e la devianza di X.

L’intercetta a (ossia il punto in cui la retta incrocia l’asse delle Y) è data da: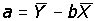

I parametri a e b identificano la retta in modo univoco.

La retta di regressione passa per il punto identificato dalle medie delle due variabili. Nel nostro esempio la retta è la seguente:

La retta di regressione è il miglior modello lineare possibile per approssimare la nube di punti ma non ci dice nulla su quanto sia buona tale approssimazione. A tale scopo è possibile calcolare il coefficiente di correlazione r, dato da: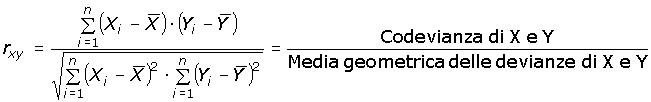

r ha la particolarità di non dipendere dall’unità di misura delle due variabili.

Vediamo alcuni casi limite. Supponendo che i 6 soggetti dell’esempio precedente siano stati sottoposti a 4 prove oggettive e abbiano ottenuto i risultati a fianco, si hanno i seguenti diagrammi di dispersione:

Massima correlazione positiva, r=+1
Massima correlazione negativa, r=-1
Assenza di correlazione, r=0

Se le variabili in questione sono standardizzate, essendo la devianza di una qualsiasi variabile standardizzata pari a n (il numero dei casi), b diventa uguale a r: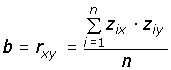

Il coefficiente di correlazione indica la forza della relazione. L’esistenza è determinata dalla significatività associata al coefficiente di correlazione. La forma viene individuata dall’esame accurato del diagramma di dispersione.

E’ possibile poi calcolare il coefficiente di determinazione, r quadro, che ci dà la proporzione della varianza riprodotta dalla regressione di Y sulla X:

sono i valori di Y riprodotti con l’equazione di regressione

r quadro è un indice di bontà di adattamento: quanto più è alto tanto minore è la somma dei quadrati dei residui dei punti dalla retta di regressione.