La Cardinalità [I1] [F1] [E1] [ES1] degli interi è aleph-zero [I1] [I2] [F1] [E1] [ES1]
Ovvero Z è un estensione di N, ma può essere messo in corrispondenza biunivoca con N.
Per esempio nel seguente modo:
[0,1] = {(0,1), (1,2), (2,3), ...(n,n + 1), ...} = -1 e così via.

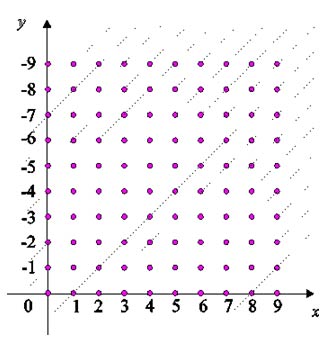
Vista ogni coppia ordinata (a,b) naturali il come un punto su N X N, i numeri interi sono le 'semirette' di coefficiente angolare 1. La bisettrice del primo quadrante (equazione y = x) corrisponde al numero 0, e divide i numeri positivi (semirette che stanno 'al di sotto' della bisettrice) dai numeri negativi (semirette 'al di sopra' della bisettrice). Possiamo sempre scegliere come rappresentante di un numero positivo la coppia (a,0), e come rappresentante di un numero negativo la coppia (0,b).