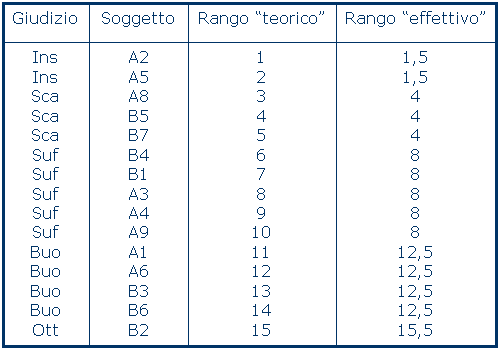
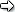Consente di comparare due serie di dati ordinali o cardinali per stabilire se esistono differenze nella localizzazione (più che nella forma) della loro distribuzione. Problema: Si può dire che vi sia una differenza statisticamente significativa nel profitto in storia tra gli allievi della 1A e della 1B? Calcoliamo il rango per ciascun valore della distribuzione congiunta delle due variabili, ai pareggi assegniamo il rango medio, ossia la media dei rispettivi ranghi: Le due distribuzioni non sono statisticamente differenti se U (U di Mann-Whitney), calcolata come è maggiore di U*, desunta dalla tavola della U di Mann-Withney (in questo caso 12), per un livello di fiducia del 95 percento e test bidirezionale. Si può dire quindi, con livello di fiducia 95 percento, che non vi siano differenze statisticamente significative tra le due distribuzioni di giudizi.
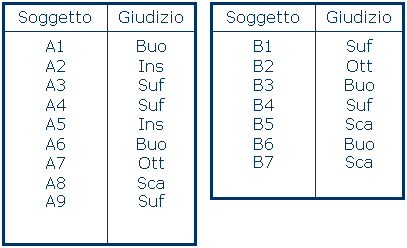
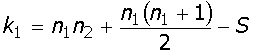 = 9*7+9*(9+1)/2-(4+4+8+8+12,5+12,5+15,5) = 43,5
= 9*7+9*(9+1)/2-(4+4+8+8+12,5+12,5+15,5) = 43,5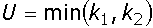 = 9*7- 43,5 = 19,5
= 9*7- 43,5 = 19,5 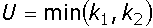 = 19,5
= 19,5
dove:
n1, n2 Numerosità dei due campioni, in questo caso n1=9 e n2=7
S Somma dei ranghi del campione più piccolo (n2)