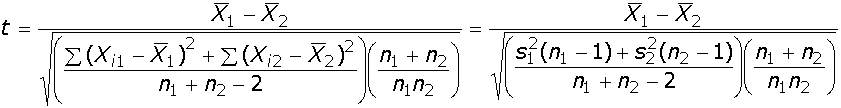Analisi dei dati

Test di differenza tra medie

Consente di rilevare la probabilità che tra le medie di una variabile cardinale rilevata su due campioni non vi sia differenza statisticamente significativa. Il test è applicabile solo se: a) le due variabili di cui si calcolano le medie si possono considerare non correlate (non presentano variazioni concomitanti negli stessi soggetti); b) la popolazione dalla quale è tratto ciascun campione si possa considerare normale (gaussiana); c) le popolazioni dalle quali sono tratti i due campioni si possono considerare omoschedastiche (ossia hanno la stessa varianza). Con due campioni di numerosità superiore ai 30 casi il secondo requisito cade dato che la distribuzione campionaria non approssima più la t di Student-Fisher (che richiede popolazioni di partenza distribuite in modo normale) ma diventa normale. Problema: In un liceo scientifico, la media della classe 1A in matematica è pari a 6,5 con uno scarto tipo di 1. La media della classe 1B è pari a 5,5 con uno scarto tipo di 2,5. La 1A ha 24 allievi e la 1B 20. Si può dire che la media delle due classi sia differente, oppure le differenze sono da attribuirsi al caso? Il problema può essere risolto con il test di differenza tra medie, che utilizza come statistica del test la t di Student-Fisher.

dove

Nel nostro caso t vale (6,5-5,5)/radq(((1^2*(24-1)+2,5^2*(20-1))/(24+20-2))*((24+20)/(24*20)))=1,8. La probabilità associata a questo valore di t, con 42 gradi di libertà e test bidirezionale ossia test a due code (dato che ci interessa sapere se la media delle due classi è differente, non se una è superiore, o inferiore, all’altra), può essere trovata con la formula Excel DISTRIB.T(1,8;42;2) e vale 0,079. La probabilità che le differenze siano da attribuirsi al caso è quindi 0,079, ossia abbastanza bassa. Per campioni di numerosità elevata (maggiore di 30 casi) la t di Student-Fisher approssima la normale standardizzata (z).

Per quanto riguarda i limiti di applicabilità, in questo esempio: a) il requisito di non correlazione è sicuramente soddisfatto dato che i due campioni (le due classi) sono formati da soggetti diversi che non si possono considerare appaiati, ossia non è possibile stabilire una corrispondenza uno a uno tra le singole rilevazioni sugli allievi dei due campioni; b) il requisito di normalità della popolazione, a meno che non siano intervenute sistematicità nel campionamento (in questo caso nella formazione delle due classi) è sicuramente soddisfatto, dato che le due classi sono tratte dalla popolazione più ampia “studenti della prima classe del liceo scientifico in Italia”, se è possibile supporre che la distribuzione della proprietà “profitto in matematica” di tale popolazione sia normale; c) il requisito di omoschedasticità si potrebbe considerare soddisfatto, a meno che non siano intervenute sistematicità nel campionamento, dato che i due campioni sono tratti dalla stessa popolazione; la differenza notevole tra i due scarti tipo dovrebbe far sorgere qualche dubbio, e suggerire ulteriori controlli sui motivi di tale differenza.

Password

109/124