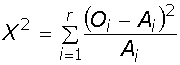Test chi quadro per una proprietà
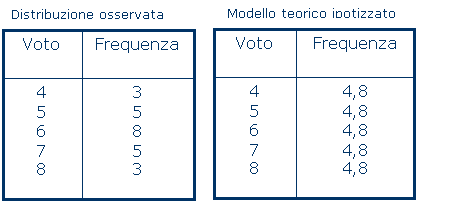
Consente di quantificare la probabilità del fatto che una distribuzione di frequenza di una serie di dati sia conforme ad un modello teorico (ad esempio il modello di equidistribuzione o quello di distribuzione normale) e decidere sulla base di tale probabilità per la conformità o meno. Problema: Data una distribuzione di frequenza qualsiasi si può dire, ad esempio, che le frequenze sono equidistribuite tra le varie categorie a meno del “rumore statistico” (errori dovuti al caso)? Questo problema si risolve calcolando la distanza del chi quadro tra il modello teorico (ossia l’equidistribuzione delle risposte omesse per tutti gli studenti) e la distribuzione osservata, con la seguente formula: Dove Il valore ottenuto di X2 (ics quadro) è un valore di ascissa della distribuzione chi quadro, al quale corrisponde una data probabilità, la probabilità che la distribuzione sotto esame si discosti dal modello teorico per effetto del caso. Il chi quadro ha in questo caso r-1 = 4 gradi di libertà, ossia siamo liberi di fissare a piacere nel nostro modello teorico 4 frequenze, ma non la quinta, dato che abbiamo come vincolo che la somma delle frequenze sia pari al numero totale dei casi (in questo caso 24). Calcolata con la formula di Excel DISTRIB.CHI(3,5;4), la probabilità che la distribuzione in esame si discosti “per caso” dal modello teorico vale 0,478.