Test chi quadro per due proprietà
Consente di quantificare la probabilità del fatto che la distribuzione della frequenza osservata in una tabella a doppia entrata sia dovuta al mero effetto del caso (in tal caso la frequenza osservata in ciascuna cella della tabella dovrebbe conincidere con la frequenza attesa) e decidere di conseguenza se vi è attrazione o repulsione tra le modalità delle due variabili oppure no. Nella tabella seguente: il chi quadro vale: dove r è il numero di celle della tabella. I vincoli sulle frequenze attese sono gli stessi del test chi quadro a una proprietà (A>1, meglio se A>5). Il numero di gradi di libertà è pari a: gdl = (num. righe –1 ) ´ (num. colonne – 1) = 1 Questo perché, come abbiamo visto, nel riempire le celle della tabella siamo liberi di scegliere tutti i valori tranne l’ultimo che è fissato dal marginale di riga o di colonna. La probabilità corrispondente a questo valore di chi quadro la si può trovare con Excel con la formula DISTRIB.CHI(7,52;1), e vale 0,0061. La probabilità che questa distribuzione congiunta sia casuale è quindi molto bassa, e ciò fa arguire che deve esserci una attrazione (o una repulsione) tra le modalità delle due variabili, attrazione che non può essere attribuita a fluttuazioni casuali. Il valore di soglia generalmente utilizzato per ritenere significativa (ossia non casuale) l’attrazione o la repulsione è 0,05. Valori di probabilità al di sotto di 0,05 fanno propendere per considerare non casuale la differenza tra frequenze osservate e frequenze attese.
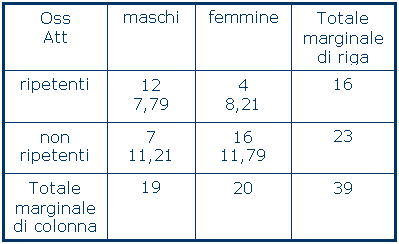
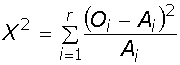= (12-7,79)^2/7,79+(4-8,21)^2/8,21+(7-11,21)^2/11,21+(16-11,79)^2/11,79 = 7,52
    Password |
|
107/124 |
|